Bagging vs. Boosting: Key Differences, Types, and Hands-on R Examples for Beginners

If you’re new to the world of machine learning, you’ve probably come across terms like “Bagging” and “Boosting” quite often.

These techniques fall under the broader umbrella of ensemble methods.

Here, the goal is to enhance model performance.

This is achieved by combining multiple “weak learners” (models that perform slightly better than random guessing) into a “strong learner.”

But what exactly are Bagging and Boosting?

And how are they different?

Let’s break it down.

What is Bagging?

Bagging, short for Bootstrap Aggregating, aims to reduce the variance in models.

Imagine you’re asking multiple people the same question to get a better answer.

Each person might have a slightly different take.

But when averaged together, their combined response is usually more accurate.

Bagging works similarly.

It creates multiple versions of the original dataset by randomly sampling with replacement (yes, a data point can appear more than once).

Then, it trains separate models (like decision trees) on these subsets.

Finally, it averages their predictions.

This process makes the model less sensitive to fluctuations in the training data. This helps reduce the chance of overfitting.

Let’s dive into some common types of Bagging techniques:

1. Random Forests:

This is the most popular form of Bagging.

Here, multiple decision trees are trained on bootstrapped datasets.

The individual predictions are averaged for the final output.

Random Forests also add randomness by selecting random subsets of features. This increases model diversity.

2. Bagged Decision Trees:

This is similar to Random Forests but without random feature selection at each node.

It uses bootstrapped datasets to train several decision trees.

The final prediction is based on the average of all trees.

3. Bagging with other models:

Bagging isn’t just limited to decision trees.

It can be applied to k-nearest neighbors (KNN), support vector machines (SVMs), or even neural networks.

The goal is to reduce variance by averaging models trained on random subsets of data.

What is Boosting?

Boosting, on the other hand, takes a different approach.

While bagging focuses on reducing variance, boosting aims to reduce bias.

This is achieved by converting weak learners into strong learners.

Imagine you’re learning to play the piano.

Each practice session focuses on your weaknesses from the previous session.

In boosting, models are trained sequentially.

Each new model corrects the errors of the previous one.

The idea is to give more weight to difficult cases that the earlier models got wrong.

This is to ensure that subsequent models pay more attention to these “tougher” examples.

In the end, the combined model is much more accurate.

Key boosting algorithms include:

1. AdaBoost (Adaptive Boosting):

This method adjusts the weights of incorrectly classified instances.

It emphasizes difficult cases in each subsequent model.

It’s simple but effective for binary classification tasks.

2. Gradient Boosting:

Instead of adjusting weights, Gradient Boosting technique builds new models sequentially.

Here, each subsequent model predicts the residuals (errors) of the previous model through gradient descent.

This helps in minimizing the overall error.

It’s more accurate but slower than AdaBoost.

3. XGBoost (Extreme Gradient Boosting):

XGBoost is a highly efficient and scalable version of gradient boosting.

It is optimized for speed and performance.

It offers advanced features like handling missing values, regularization, parallel processing, and tree pruning.

4. LightGBM:

This gradient boosting variant uses histogram-based techniques to split trees faster.

This makes it suitable for large datasets.

It splits the trees leaf-wise, improving efficiency and speed.

5. CatBoost (Categorical Boosting):

CatBoost is designed to handle categorical features efficiently.

It, therefore, often outperforms other boosting algorithms when dealing with structured data.

It automatically handles missing values and categorical variables without extensive preprocessing.

This makes it more user-friendly.

Key Differences Between Bagging and Boosting

Let’s summarize the differences between these two techniques in a handy table:

Aspect	Bagging	Boosting
Training Process	Models are trained independently and in parallel on different subsets of data.	Models are trained sequentially, with each new model correcting errors of the previous one.
Focus	Reduces variance by averaging multiple models' outputs.	Reduces bias by giving more focus to misclassified instances in subsequent models.
Overfitting Risk	Less prone to overfitting, as models work independently and predictions are averaged.	Higher risk of overfitting, especially with too many iterations, as it focuses heavily on hard-to-predict cases.
Model Diversity	Uses multiple base models trained on bootstrapped data (e.g., Random Forests).	Uses a sequence of models, each improving on the errors of the previous one (e.g., AdaBoost, XGBoost).
Example Algorithms	Random Forests, Bagged Decision Trees, Bagged SVMs.	AdaBoost, Gradient Boosting, XGBoost, LightGBM, CatBoost.
Data Handling	Handles noisy data better due to independent training of models.	May be sensitive to noise, as models focus more on difficult instances.
Performance	Generally stabilizes performance, making models more robust across different datasets.	Often results in more accurate predictions but requires careful tuning to avoid overfitting.
Complexity	Simple implementation; parallelizable, making it faster to train.	More complex due to sequential training; harder to parallelize and often slower to train.

When to Use Bagging vs. Boosting?

Use Bagging when your model is prone to overfitting.

It is especially the case when you are working with high-variance models like decision trees.

Random Forests, for example, are a great choice when you want stable predictions across various datasets.

Use Boosting when you have a high bias problem.

That means where your model consistently performs poorly across different datasets, Boosting helps improve the performance.

Moreover, if you need more precise predictions and are willing to tweak hyperparameters, boosting is the way to go.

Practical Example: Predicting Student Exam Performance

Let’s say you’re trying to predict whether a student will pass or fail an exam based on study hours, attendance, and assignment scores.

In bagging, you’d create multiple subsets of this data.

Then, you’d train separate decision trees on each of the data subsets.

Finally, you’d combine their results for a more reliable prediction.

In boosting, you’d start with a simple decision tree.

Identify where it went wrong.

Then, build another tree that tries to fix those mistakes.

You’d be repeating this process several times.

Here’s a simple demonstration of both Bagging (Random Forests) and Boosting (XGBoost) in R.

First, let’s get to the Bagging Model

Step 1: Load necessary libraries

install.packages(c("caret", "randomForest", "smotefamily", "xgboost", "adabag"))

library(caret)
library(randomForest)
library(xgboost)
library(smotefamily)
library(adabag)

The first line installs multiple R packages necessary for the analysis.

Each package serves a unique purpose:

caret: Provides a unified interface for machine learning tasks, such as data partitioning and model evaluation.
randomForest: Implements the Random Forest algorithm for classification and regression tasks.
smotefamily: Offers tools for balancing datasets using SMOTE (Synthetic Minority Over-sampling Technique).
xgboost: Implements the XGBoost (Extreme Gradient Boosting) algorithm, a powerful boosting technique.
adabag: Provides the AdaBoost algorithm, another boosting technique.

Each of the subsequent lines loads the respective installed libraries into the R environment.

This makes their functions accessible for use.

Step 2: Prepare the Dataset

# Example dataset: Simulating student data
set.seed(123)
data <- data.frame(
  Study_Hours = runif(200, 1, 10),
  Attendance = sample(50:100, 200, replace = TRUE),
  Assignment_Scores = sample(1:100, 200, replace = TRUE),
  Pass = sample(c(0, 1), 200, replace = TRUE)
)

This block creates a synthetic dataset of 200 students with four variables:

Study_Hours: A continuous variable generated using runif() to randomly assign study hours between 1 and 10.
Attendance: An integer variable generated using sample() to represent attendance percentages, randomly chosen between 50 and 100.
Assignment_Scores: An integer variable representing assignment scores, randomly selected between 1 and 100.
Pass: A binary target variable (0 or 1) indicating whether a student has passed or failed, generated using sample() with replacement.

The function set.seed(123) is used to make the random values reproducible. It ensures that each time you run the code, you get the same dataset.

Step 3: Split the Dataset into Training and Testing Sets

# Split data into training and testing sets 
set.seed(123) 
trainIndex <- createDataPartition(data$Pass, p = 0.7, list = FALSE) 
trainData <- data[trainIndex,] 
testData <- data[-trainIndex,]

This block divides the data into training and testing sets:

createDataPartition(): It is part of the caret package.
It splits the dataset based on the target variable (Pass) to ensure an even distribution of classes in both sets.
p = 0.7: Specifies that 70% of the data should be used for training, and the remaining 30% for testing.
The result is two datasets: trainData (70% of the original data) and testData (30%).

Step 4: Convert the Target Variable to a Factor

# Convert 'Pass' to a factor to perform classification 
trainData$Pass <- as.factor(trainData$Pass) 
testData$Pass <- as.factor(testData$Pass)

These lines convert the Pass variable in both the training and testing sets to a factor.

This step is necessary because classification algorithms in R, such as Random Forest, expect the target variable to be a factor for categorical predictions.

Step 5: Train a Simple Random Forest Model

# Train a simple Random Forest model for classification
set.seed(123)
rf_model <- randomForest(Pass ~ ., data = trainData, ntree = 20)

This line trains a Random Forest model on the training data:

Pass ~ .: Specifies that Pass is the target variable, and all other columns (~ .) are predictors.
data = trainData: The model is trained on the trainData dataset.
ntree = 20: Sets the number of decision trees in the Random Forest to 20.
This example uses a simple dataset.
Here, ntree = 20 has been arrived at, after trial & error, since it gave the optimum performance.
In general, however, higher values often yield better accuracy.
set.seed(123) is used to ensure reproducibility of results.

Step 6: Make Predictions with the Random Forest Model

# Predict on test data 
rf_pred <- predict(rf_model, newdata = testData)

This line uses the trained Random Forest model to make predictions on the test dataset:

predict(): A function that applies the trained model to new data.
newdata = testData: Specifies the test dataset on which predictions are made.
The result, rf_pred, contains the predicted classes (0 or 1) for each observation in the test set.

Step 7: Evaluate Model Performance with a Confusion Matrix

# Evaluate model performance 
rf_confusion <- confusionMatrix(rf_pred, testData$Pass) 
print(rf_confusion)

This block evaluates the model’s performance using a confusion matrix:

confusionMatrix(): A function from the caret package that calculates performance metrics like accuracy, sensitivity, and specificity.
rf_pred: The predicted classes from the model.
testData$Pass: The actual classes in the test dataset.
print(rf_confusion): Displays the confusion matrix and metrics.
These help us assess the model’s performance.

The output of the above simple Random Forest Model

Interpretation of the output

The confusion matrix and performance metrics shown in the output provide insights into how well the Random Forest model performed on the test dataset.

Here’s an interpretation of each key metric:

Confusion Matrix

The confusion matrix provides the following breakdown:

True Positives (TP) (0 predicted as 0): 21
False Negatives (FN) (1 predicted as 0): 15
False Positives (FP) (0 predicted as 1): 9
True Negatives (TN) (1 predicted as 1): 15

Key Performance Metrics

Accuracy: 0.6 (or 60%)
- Interpretation: The model correctly classified 60% of the test instances.
- No Information Rate (NIR): 0.6.
  It means that a model that always predicts the majority class would also have 60% accuracy.
  The P-value (0.5558) indicates that the model’s accuracy is not significantly better than the NIR.
Kappa: 0.2
- Interpretation: Kappa measures the agreement between predicted and actual classes, adjusting for chance.
  A Kappa of 0.2 is quite low. It indicates poor agreement beyond random chance.
Sensitivity (Recall for class 0): 0.5833 (58.33%)
- Interpretation: The model correctly identified 58.33% of the instances where the actual class was 0.
Specificity (Recall for class 1): 0.625 (62.5%)
- Interpretation: The model correctly identified 62.5% of the instances where the actual class was 1.
Positive Predictive Value (Precision for class 0): 0.7 (or 70%)
- Interpretation: When the model predicted class 0, it was correct 70% of the time.
Negative Predictive Value (Precision for class 1): 0.5 (or 50%)
- Interpretation: When the model predicted class 1, it was correct only 50% of the time.
Balanced Accuracy: 0.6042 (or 60.42%)
- Interpretation: Balanced accuracy is the average of sensitivity and specificity. It accounts for class imbalance.
  Here, its value above shows it is slightly above the chance level.
  This tells us that the model’s predictions, in this case, are only marginally better than random guessing.

To sum up, the model’s accuracy is 60%, which is not better than the No Information Rate (NIR) of 60%.

Additionally, the Kappa score of 0.2 indicates weak agreement between predictions and actual outcomes.
This suggests that the model is not performing well in distinguishing between the classes.

Possible Improvements

Hyperparameter Tuning: Increase ntree (number of trees) or tune other parameters like mtry to see if it improves the model’s accuracy.
Try Boosting Algorithms: Boosting techniques, such as XGBoost or AdaBoost, might improve the model’s performance by focusing on misclassified instances.
Feature Engineering: Create additional features or interactions that might better capture patterns in the data.
Increase Training Data: With a larger or more informative dataset, the model might learn more discriminative patterns.

Let’s try to improve the above Model (steps 5 to 7 above) using Hyperparameter Tuning.

Hyperparameter Tuning of Random Forest Using a Manual Grid Search

This method involves a manual grid search approach for tuning the mtry parameter in a Random Forest model.

It optimizes mtry by testing multiple values.

Then, it selects the one that yields the highest accuracy on the test set.

It then trains a final model with the optimal mtry.

This approach aims to improve the model’s classification performance.

The performance is then evaluated using a confusion matrix.

Below is the block of code and its explanation.

# Define a range of mtry values to test
mtry_values <- seq(1, ncol(trainData) - 1, by = 1)

This line defines a sequence of values for the mtry parameter.

This parameter specifies the number of variables considered at each split in the Random Forest trees.

The seq() function creates a sequence:

1 is the starting value.
ncol(trainData) - 1 is the end value.
It ensures we try up to the maximum possible features minus one (as mtry cannot exceed the number of predictor variables).
by = 1 increments the sequence by one for each step.

This range allows us to explore different values of mtry to find the optimal one.

# Perform manual grid search for mtry
set.seed(123)
results <- sapply(mtry_values, function(mtry_val) {
  model <- randomForest(Pass ~ ., data = trainData, ntree = 19, mtry = mtry_val)
  mean(predict(model, testData) == testData$Pass)
})

This block performs a manual grid search over the defined mtry_values:

set.seed(123): Ensures reproducibility of results.
sapply(): Applies a function over each value in mtry_values. It stores the results in a vector called results.
Inside the sapply() function:
- A Random Forest model is trained using randomForest() with the specified mtry value (mtry = mtry_val) and ntree = 19 (19 trees).
- The model is evaluated by predicting on the test dataset.
  mean(predict(model, testData) == testData$Pass) calculates the accuracy for each mtry value.
The output is a vector results .
Each element in it represents the accuracy corresponding to an mtry value.

# Find the best mtry value based on test accuracy
optimal_mtry <- mtry_values[which.max(results)]
cat("Optimal mtry:", optimal_mtry, "\n")

This block finds the mtry value that yielded the highest accuracy on the test set:

which.max(results): Finds the index of the maximum value in results (the best accuracy).
mtry_values[which.max(results)]: Extracts the mtry value corresponding to the highest accuracy.
cat("Optimal mtry:", optimal_mtry, "\n"): Prints the optimal mtry value to the console.

This optimal mtry will be used to retrain the Random Forest model.

# Train a Random Forest model with tuned parameters
set.seed(123)
rf_model_tuned <- randomForest(Pass ~ ., data = trainData, ntree = 19, mtry = optimal_mtry)

This line retrains the Random Forest model with the tuned mtry parameter:

Pass ~ .: Specifies that Pass is the target variable, and all other columns are predictors.
data = trainData: Uses the training dataset.
ntree = 19: Sets the number of trees to 19.
mtry = optimal_mtry: Uses the best mtry value identified from the grid search.
set.seed(123): Ensures reproducibility of the trained model.

This model is expected to now perform better, as mtry has been optimized for accuracy.

# Predict on test data
rf_pred_tuned <- predict(rf_model_tuned, newdata = testData)

This line makes predictions on the test dataset using the tuned Random Forest model:

predict(): Applies the rf_model_tuned model to testData.
newdata = testData: Specifies the data on which to make predictions (the test set).
The predictions are stored in rf_pred_tuned.

# Evaluate model performance
rf_confusion_tuned <- confusionMatrix(rf_pred_tuned, testData$Pass)
print(rf_confusion_tuned)

This block evaluates the performance of the tuned model:

confusionMatrix(): Computes a confusion matrix and other performance metrics (e.g., accuracy, sensitivity, specificity).
This is done by comparing predicted and actual values.
rf_pred_tuned: The predicted classes from the tuned Random Forest model.
testData$Pass: The actual classes in the test dataset.
print(rf_confusion_tuned): Displays the confusion matrix and metrics.
These allow us to assess how well the model performed after tuning.

The output after performing Hyperparameter Tuning of the Random Forest Model

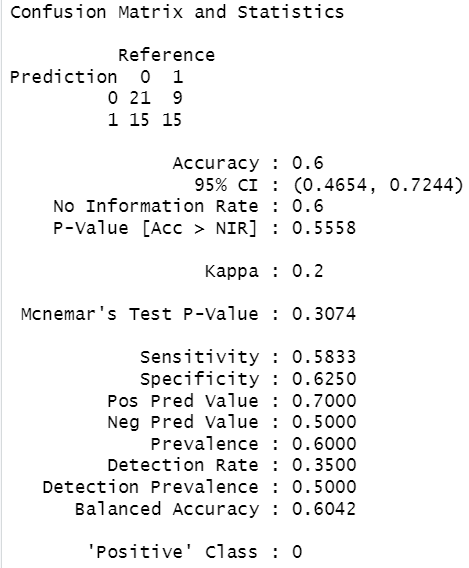
The above output is a result of tuning the mtry parameter.

It shows that despite Hyperparameter tuning, the model’s performance metrics (accuracy, sensitivity, specificity, etc.) remain the same as the initial model.

One possible cause could be that the dataset may lack strong patterns or features that distinguish between classes. This tends to limit the model’s ability to learn effectively.

It could also be that there may be underfitting.

In simple terms, underfitting means there is a lack of sufficient information in the dataset for the model to leverage.

Let’s first check the class imbalance in the dataset (i.e., whether there is any possibility of underfitting).

The following code helps check the class imbalance.

# Check class distribution in the original training data
table(trainData$Pass)

In this case, the above code resulted in the following output:

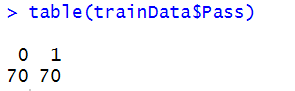
This shows that in the training data, there are 70 instances of class 0 and 70 of class 1.

So, class imbalance (i.e., underfitting) is not an issue here.

In our case, the synthetic dataset has been created to illustrate the concepts of Bagging and Boosting.

The dataset may be lacking complex relationships or strong patterns between the predictors (Study_Hours, Attendance, Assignment_Scores) and the target variable (Pass).

K-fold cross-validation

Remember, our aim here is to get a more robust measure of model performance.

Let’s see if k-fold cross-validation helps us in this direction.

In general, it ensures the model’s accuracy isn’t overly dependent on a single train-test split.

# Define cross-validation settings (10-fold cross-validation)
train_control <- trainControl(
  method = "cv",          # Cross-validation
  number = 10,            # Number of folds
  verboseIter = TRUE      # Print training log
)

# Train the Random Forest model with cross-validation
set.seed(123)
rf_cv_model <- train(
  Pass ~ .,               # Model formula (target ~ predictors)
  data = trainData,       # Training dataset
  method = "rf",          # Random Forest model
  trControl = train_control,  # Cross-validation settings
  tuneGrid = data.frame(mtry = optimal_mtry),  # Use the optimal mtry value
  ntree = 200             # Number of trees
)

# Display cross-validation results
print(rf_cv_model)

# Check average cross-validated accuracy
rf_cv_model_results <- rf_cv_model$results
cat("Cross-validated accuracy:", rf_cv_model_results$Accuracy, "\n")

Here, the cross-validation settings of trainControl() defines a 10-fold cross-validation using method = "cv" and number = 10.
The setting verboseIter = TRUE provides feedback during training.

After performing the cross-validation, the last line of code extracts the average cross-validated accuracy across all folds, providing a single measure of the model’s performance.

In this case, the cross-validation gave the following output:

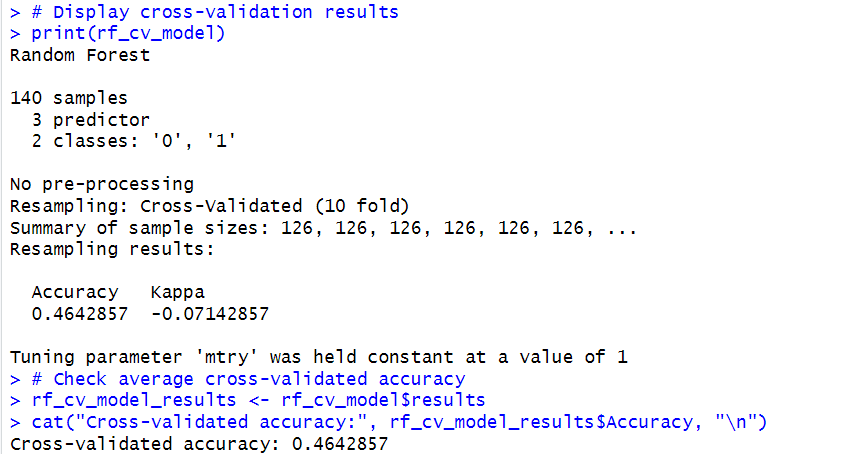
The above results show that the current model configuration does not effectively capture patterns in the data.

As mentioned above, in our case, there might not be enough information in the features to make accurate predictions.

This may be causing the model’s performance constraints in our simplistic dataset example.

In general, you can follow the following steps to try to improve the model performance:

Increase the Number of Trees: Increase ntree in the Random Forest model to around 100 or 200.
A larger forest can sometimes capture subtler patterns if they exist.
In our example, ntree = 20 gave the optimum result. This may be due to the simplistic nature of the data.
Feature Engineering: Create new features that might have a stronger relationship with Pass.
For example, you could create interaction terms or transformations of existing variables (like square of Study_Hours or interaction between Study_Hours and Attendance).

Moving on to the Boosting Models

Let’s first start with the AdaBoost Model.

The steps 1 to 3 are the same as those performed previously for Bagging.

They are reproduced below for clarity.

Step 1: Load necessary libraries

install.packages(c("caret", "randomForest", "smotefamily", "xgboost", "adabag"))

library(caret)
library(randomForest)
library(xgboost)
library(smotefamily)
library(adabag)

Step 2: Prepare the Dataset

# Example dataset: Simulating student data
set.seed(123)
data <- data.frame(
  Study_Hours = runif(200, 1, 10),
  Attendance = sample(50:100, 200, replace = TRUE),
  Assignment_Scores = sample(1:100, 200, replace = TRUE),
  Pass = sample(c(0, 1), 200, replace = TRUE)
)

Step 3: Split the Dataset into Training and Testing Sets

# Split data into training and testing sets 
set.seed(123) 
trainIndex <- createDataPartition(data$Pass, p = 0.7, list = FALSE) 
trainData <- data[trainIndex,] 
testData <- data[-trainIndex,]

Step 4: Implementing AdaBoost

# Check structure to ensure 'Pass' is a factor
str(trainData)

This line checks the structure of trainData using str().

Ensure that the Pass variable is a factor is critical.

This is because AdaBoost in adabag expects the target variable to be categorical (factor format).

# Ensure there are no missing values in the training data
trainData <- na.omit(trainData)

This line removes any missing values from the training dataset using na.omit().

Missing values can cause issues in model training.

This is true especially in boosting algorithms, as they rely on a sequence of weak learners.

Ensuring a clean dataset helps avoid unexpected errors during training.

# Train AdaBoost model using the 'adabag' package
set.seed(123)
ada_model <- boosting(
  Pass ~ .,          # Formula for the model
  data = trainData,  # Training dataset
  boos = TRUE,       # Boosting enabled
  mfinal = 10        # Number of boosting iterations
)

This block of code trains an AdaBoost model with the following settings:

set.seed(123): Ensures reproducibility of the results.
boosting(): A function from the adabag package that implements AdaBoost.
- Pass ~ .: Specifies that Pass is the target variable, and all other variables in the dataset are predictors.
- data = trainData: Uses trainData as the training dataset.
- boos = TRUE: Enables boosting; this parameter ensures that the algorithm focuses more on misclassified instances in each iteration.
- mfinal = 10: Specifies the number of boosting iterations (weak learners or decision stumps) the model will use.
  A higher mfinal value often improves accuracy but also increases computation time.
  Here, mfinal = 10 is used for faster training and demonstration purposes.

# Predict on the test data
ada_pred <- predict(ada_model, newdata = testData)

This line makes predictions on the test dataset:

predict(): Uses the trained AdaBoost model to predict the classes for new data.
ada_model: The trained AdaBoost model.
newdata = testData: Specifies that predictions should be made on testData.
The result, ada_pred, is an object that contains predicted classes and additional details about the predictions.

# Extract the predicted classes
ada_pred_class <- ada_pred$class

This line extracts the predicted class labels from the ada_pred object.

The predict() function in adabag returns several elements, including probabilities and predicted classes.

Here, ada_pred$class contains only the predicted classes (0 or 1), which are stored in ada_pred_class.

# Evaluate model performance using a confusion matrix
ada_confusion <- confusionMatrix(factor(ada_pred_class), factor(testData$Pass))
print(ada_confusion)

This block evaluates the model’s performance using a confusion matrix:

confusionMatrix(): Part of the caret package.
This function calculates performance metrics like accuracy, sensitivity, and specificity by comparing predicted and actual values.
- factor(ada_pred_class): Converts the predicted classes to a factor to match the format of the actual classes.
- factor(testData$Pass): Converts the actual classes in testData to a factor.
print(ada_confusion): Displays the confusion matrix, showing key performance metrics for the model.

Here’s an explanation of the key steps and concepts of the AdaBoost Model.

AdaBoost Training: AdaBoost focuses on misclassified samples in each iteration.
It gives them higher weights so that subsequent models focus more on hard-to-predict instances.
Predictions: The model predicts classes for the test set, and only the predicted class labels are extracted for evaluation.
Confusion Matrix: The confusion matrix evaluates model performance by comparing the predicted and actual classes.
It provides insights into metrics like accuracy, sensitivity, and specificity.

The output of the above AdaBoost Model

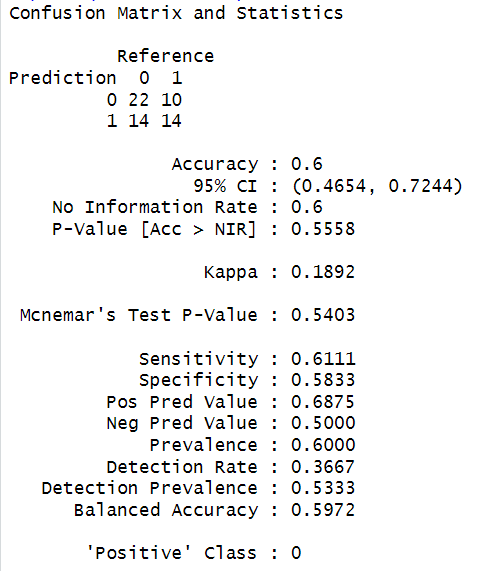
For our example, the AdaBoost model has achieved similar results to previous models, with 60% accuracy.

One thing to note here.

The outputs for the AdaBoost model show variations in performance with different numbers of boosting rounds.

Initially, fewer boosting rounds (= 5) were considered.

This resulted in a higher sensitivity (69.44%) for class 0. This shows it is relatively better at identifying instances of class 0.

However, it gave a lower specificity (41.67%) for class 1. That means a poor detection of class 1 instances.

So, with fewer boosting rounds, the model focuses more on detecting class 0 but at the cost of accuracy for class 1.

Similarly, when boosting rounds were increased to 20 in this case, we found the opposite result.

Now, the Sensitivity dropped to 55.56%. This indicated that the model has become less effective at identifying class 0 instances.

At the same time, Specificity improved to 58.33%. This means that it now detects class 1 better.

So, there is a trade-off between Sensitivity and Specificity when we change the boosting rounds.

Now, let’s go with the XGBoost Model.

Steps 1 to 3 are the same again.

Step 1: Load necessary libraries

install.packages(c("caret", "randomForest", "smotefamily", "xgboost", "adabag"))

library(caret)
library(randomForest)
library(xgboost)
library(smotefamily)
library(adabag)

Step 2: Prepare the Dataset

# Example dataset: Simulating student data
set.seed(123)
data <- data.frame(
  Study_Hours = runif(200, 1, 10),
  Attendance = sample(50:100, 200, replace = TRUE),
  Assignment_Scores = sample(1:100, 200, replace = TRUE),
  Pass = sample(c(0, 1), 200, replace = TRUE)
)

Step 3: Split the Dataset into Training and Testing Sets

# Split data into training and testing sets 
set.seed(123) 
trainIndex <- createDataPartition(data$Pass, p = 0.7, list = FALSE) 
trainData <- data[trainIndex,] 
testData <- data[-trainIndex,]

Step 4: Implementing XGBoost

# Prepare data matrices for XGBoost
train_matrix <- xgb.DMatrix(data = as.matrix(trainData[, -4]), label = trainData$Pass)
test_matrix <- xgb.DMatrix(data = as.matrix(testData[, -4]), label = testData$Pass)

XGBoost requires data to be in a specific matrix format called DMatrix. This block prepares the data accordingly:

as.matrix(trainData[, -4]): Converts the training predictors (all columns except Pass) to a matrix format.
trainData$Pass: Sets the target variable (Pass) for the training set.
xgb.DMatrix(): Creates an XGBoost DMatrix for both training and testing data.
This optimizes memory usage and computation speed.

# Set the parameters for XGBoost
params <- list(
  booster = "gbtree",
  objective = "binary:logistic",  # For binary classification
  eval_metric = "error"           # Error rate as evaluation metric
)

This code defines the parameters for the XGBoost model:

booster = "gbtree": Specifies that the model should use decision trees as base learners.
objective = "binary:logistic": Sets the objective for binary classification with logistic regression, meaning the model will output probabilities for each class.
eval_metric = "error": Uses error rate as the evaluation metric, which calculates the proportion of incorrect predictions.

# Train the XGBoost model
set.seed(123)
xgb_model <- xgboost(
  data = train_matrix,
  params = params,
  nrounds = 200,  # Number of boosting rounds
  verbose = 0     # No verbose output
)

This block trains the XGBoost model using the defined parameters:

set.seed(123): Ensures reproducibility of the training process.
xgboost(): Trains the XGBoost model with specified parameters.
- data = train_matrix: Uses the training data matrix.
- params = params: Applies the previously defined parameters.
- nrounds = 200: Sets the number of boosting rounds (iterations) to 200. A higher number allows the model to capture complex patterns but increases computation time.
- verbose = 0: Suppresses verbose output, keeping the training output minimal.

# Predict on the test data
xgb_pred <- predict(xgb_model, newdata = test_matrix)

This line makes predictions on the test dataset:

predict(): Uses the trained XGBoost model to make predictions.
newdata = test_matrix: Specifies the test data matrix.
The output, xgb_pred, contains the predicted probabilities for each instance in the test set.

# Convert probabilities to binary predictions (0 or 1)
xgb_pred <- ifelse(xgb_pred > 0.5, 1, 0)

Since the XGBoost model outputs probabilities, this line converts them to binary predictions:

ifelse(xgb_pred > 0.5, 1, 0): Applies a threshold of 0.5, assigning a class label of 1 if the probability is greater than 0.5, and 0 otherwise.

# Evaluate model performance using a confusion matrix
xgb_confusion <- confusionMatrix(factor(xgb_pred), factor(testData$Pass))
print(xgb_confusion)

This block evaluates the model’s performance using a confusion matrix:

confusionMatrix(): Part of the caret package.
This function calculates performance metrics like accuracy, sensitivity, and specificity by comparing predicted and actual values.
- factor(xgb_pred): Converts the predicted binary classes to a factor for compatibility.
- factor(testData$Pass): Converts the actual test classes to a factor.
print(xgb_confusion): Displays the confusion matrix and key metrics. It allows us to assess the model’s effectiveness in classifying the test data.

Here’s an explanation of the key steps and concepts of the XGBoost Model.

Boosting in XGBoost: XGBoost is an ensemble algorithm that combines multiple weak learners to create a strong classifier.
Each boosting round tries to correct the errors of the previous round.
Binary Classification: The binary:logistic objective optimizes for binary outcomes, with the output being probabilities between 0 and 1.
Thresholding for Binary Predictions: The model’s output probabilities are converted to binary class labels using a threshold of 0.5.

The output of the above XGBoost Model

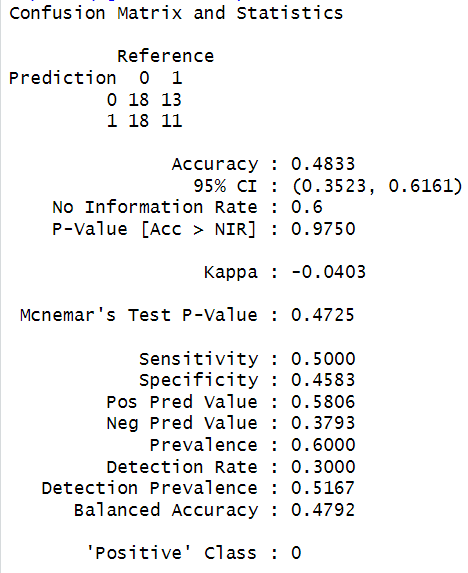
This output suggests that, with the current dataset and configuration, XGBoost has not effectively modeled the target variable.

In general, we can try to improve the performance of XGBoost by Parameter Tuning.

In it, we perform hyperparameter tuning for XGBoost, including parameters like max_depth, eta (learning rate), subsample, and colsample_bytree.

Let’s summarize both Bagging and Boosting Models.

In this example, Bagging (Random Forest) combines the predictions of multiple decision trees trained on random samples.

This leads to a stable performance by reducing overfitting.

Boosting (XGBoost), on the other hand, sequentially corrects errors.

It often leads to more accurate but potentially more complex models.

In Conclusion

Bagging and Boosting are both powerful ensemble techniques, but they cater to different challenges in machine learning.

Bagging helps to make your model more stable by reducing variance.

On the other hand, boosting makes your model smarter by addressing bias.

Bagging and Boosting can be used independently.

It’s also possible to combine them with other techniques. This may ensure better results, depending on the problem at hand.

Remember, the key to mastering these techniques lies in understanding your dataset, evaluating model performance, and fine-tuning hyperparameters.

Bagging vs. Boosting: Key Differences, Types, and Hands-on R Examples for Beginners

What is Bagging?

Let’s dive into some common types of Bagging techniques:

1. Random Forests:

2. Bagged Decision Trees:

3. Bagging with other models:

What is Boosting?

1. AdaBoost (Adaptive Boosting):

2. Gradient Boosting:

3. XGBoost (Extreme Gradient Boosting):

4. LightGBM:

5. CatBoost (Categorical Boosting):

Key Differences Between Bagging and Boosting

When to Use Bagging vs. Boosting?

Practical Example: Predicting Student Exam Performance

First, let’s get to the Bagging Model

Step 1: Load necessary libraries

Step 2: Prepare the Dataset

Step 3: Split the Dataset into Training and Testing Sets

Step 4: Convert the Target Variable to a Factor

Step 5: Train a Simple Random Forest Model

Step 6: Make Predictions with the Random Forest Model

Step 7: Evaluate Model Performance with a Confusion Matrix

The output of the above simple Random Forest Model

Interpretation of the output

Here’s an interpretation of each key metric:

Confusion Matrix

Key Performance Metrics

Possible Improvements

Hyperparameter Tuning of Random Forest Using a Manual Grid Search

The output after performing Hyperparameter Tuning of the Random Forest Model

K-fold cross-validation

Moving on to the Boosting Models

Let’s first start with the AdaBoost Model.

Step 1: Load necessary libraries

Step 2: Prepare the Dataset

Step 3: Split the Dataset into Training and Testing Sets

Step 4: Implementing AdaBoost

The output of the above AdaBoost Model

Now, let’s go with the XGBoost Model.

Step 1: Load necessary libraries

Step 2: Prepare the Dataset

Step 3: Split the Dataset into Training and Testing Sets

Step 4: Implementing XGBoost

The output of the above XGBoost Model

Let’s summarize both Bagging and Boosting Models.

In Conclusion

Further Reading and References

Submit a Comment Cancel reply