Understanding Kurtosis: A Deeper Dive into Data Distribution

by | Sep 12, 2023 | Data Analytics

  Hey there, data explorers! 📊 Have you ever wondered what secrets your data holds beyond the usual suspects like mean and standard deviation? Well, it’s time to shine the spotlight on a lesser-known but equally fascinating statistic: Kurtosis. It’s like the hidden gem of data analysis, revealing the intriguing stories lurking within your datasets. Kurtosis isn’t just about dry numbers; it’s the Sherlock Holmes of statistics, helping us uncover the mysteries of data distributions. In this blog post, we’re going to embark on a journey to demystify kurtosis. We’ll unravel what kurtosis is, the different types it comes in, and how to calculate it using R. But wait, there’s more! We’ll also delve into the world of kurtosis plots, visualizing data like never before. So, if you’re ready to go beyond the basics and explore the thrilling world of kurtosis, fasten your seatbelts. We’re about to dive into the heart of data distribution and uncover the stories that numbers can tell. Let’s get started! 🚀

What Is Kurtosis?

Kurtosis is a statistical measure that describes the shape of the probability distribution of a dataset. It quantifies the “tailedness” or the thickness of the tails and the peakedness of the distribution. In essence, kurtosis tells us how much data is in the tails compared to the center of the distribution.

Types of Kurtosis

Kurtosis comes in three main flavors:

  1. Mesokurtic: This is the baseline kurtosis and occurs when the data distribution exhibits the same tail behavior as a normal distribution.It has a kurtosis value (usually denoted by the symbol ‘k’) of 0. This tells you that you are looking at a distribution with average tail thickness.
  2. Leptokurtic: A leptokurtic distribution has positive kurtosis (k > 0).You’re now looking at a distribution that has heavier tails and a sharper peak compared to a normal distribution. This tells you that there’s a higher likelihood of extreme values or outliers.
  1. Platykurtic: A platykurtic distribution has negative kurtosis (k < 0).Just the opposite of what you’d expect from the previous Leptokurtic distribution. That means it has lighter tails and a flatter peak than a normal distribution. Such distributions indicate that you have a lower likelihood of extreme values.

How to Calculate Kurtosis

Here’s the formula to calculate the kurtosis of a given sample of data.

Kurtosis = (Σ(xi - x̄)^4 / n) / s^4

where:

    • Σ represents the summation symbol (sum of all values)
    • xi is each individual data point
    • x̄ is the sample mean
    • n is the number of data points
    • s is the sample standard deviation

How to Calculate Kurtosis using R programming language

Want to calculate the Kurtosis of a distribution? Well, here are two of the common methods in R that you can use:

1. Using the ‘Kurtosis’ Function from the ‘Moments’ Package

In R, you can use the kurtosis function from the moments package to calculate excess kurtosis, which measures the kurtosis relative to a normal distribution. The above package applies the following formula to give you the Kurtosis value:

Excess Kurtosis = (M4 / M2^2) - 3

Where M4 is the fourth moment and M2 is the second moment (variance) of the data. The kurtosis function computes these moments and then applies the formula to calculate excess kurtosis. By subtracting 3 from the result, it provides a measure of kurtosis relative to a normal distribution. A value of 0 indicates that the distribution has the same kurtosis as a normal distribution (mesokurtic). On the other hand, positive values indicate heavier tails (leptokurtic), and negative values indicate lighter tails (platykurtic). Here’s how you can use the kurtosis function:

R code
# Load the 'moments' package
library(moments)
install.packages("moments")
library(moments)
# Sample data (replace with your own dataset)
data <- c(12, 15, 18, 22, 25, 28, 31, 35, 38, 41)
# Calculate excess kurtosis using the 'kurtosis' function
excess_kurtosis <- kurtosis(data)
# Print the result
print(excess_kurtosis)
In the above code, you can replace the data vector with your own dataset to obtain the Kurtosis value of your dataset.
Here’s the output you will get from the above sample data:

The above result is the excess kurtosis value. It is a measure of how the kurtosis of your data (in this case, the above sample data) differs from that of a normal distribution.

2. Direct Calculation

There’s another way you can calculate kurtosis. And that’s by directly using the formula:

Kurtosis = (Σ(xi - x̄)^4 / n) / s^4

Where xi represents each individual data point, x̄ is the sample mean, n is the number of data points, and s is the sample standard deviation.

R code
# Sample data (replace this with your dataset)
data <- c(12, 15, 18, 22, 25, 28, 31, 35, 38, 41)
# Calculate sample mean and standard deviation
mean_data <- mean(data)
sd_data <- sd(data)
# Calculate kurtosis using the formula
n <- length(data)
kurt <- sum((data - mean_data)^4) / (n * sd_data^4)
print(kurt)

In the above code, you can replace the data vector with your own dataset to obtain the Kurtosis value of your dataset.

  Here’s the output you will get from the above sample data:

Why the hell, are the above two results different??

Well, if you get different results using the above methods, don’t press the panic button!! The reason you might obtain different results when calculating kurtosis using the kurtosis function from the moments package and the direct calculation is due to the different formulas and definitions of kurtosis used by these methods. Here’s what it means.

  1. Using the kurtosis function from the moments package:
    • The kurtosis function from the moments package calculates what is known as “sample excess kurtosis.”This means it calculates the kurtosis of your data relative to a normal distribution.It subtracts 3 from the kurtosis value to obtain excess kurtosis, so a normal distribution has a kurtosis of 0 (mesokurtic).Positive values indicate leptokurtic distributions (heavier tails), and negative values indicate platykurtic distributions (lighter tails).
  2. Direct Calculation:
    • The direct calculation of kurtosis using the formula provided above, calculates the “sample kurtosis” without subtracting 3.This means it measures the kurtosis of your data as it is, without reference to a normal distribution.As a result, this method can yield different values than the kurtosis function, especially if your data deviates from a normal distribution.

Which method should you use then??

Well, it depends on what you want to measure:

  • If you want to assess how your data’s kurtosis compares to a normal distribution, you may prefer the kurtosis function from the moments package. Because it provides excess kurtosis values.
  • On the other hand, if you want to calculate kurtosis in its original form without reference to normality, the direct calculation is more appropriate.

It’s important that you choose the method that aligns with your specific analytical goals and how you want to interpret kurtosis in your data. Also, ensure that you’re using the same method consistently when comparing and analyzing datasets or results.

How to interpret the Kurtosis values

Well, it’s pretty simple! In general,

  • High positive kurtosis ( typically, kurtosis values above 3 ) suggests that data has fat tails and is more prone to extreme values.
  • Low negative kurtosis ( typically, kurtosis values below (-3) ) suggests that data has thin tails and is less prone to extreme values.
  • A value of zero indicates that the data has a similar tail behavior as a normal distribution.

Now, it’s important for you to note that while the above ranges are commonly used as guidelines, the interpretation of kurtosis should also consider the specific context and domain of the data. Additionally, know that different statistical software or methods may yield slightly different ranges for categorizing kurtosis.

Visualizing Kurtosis

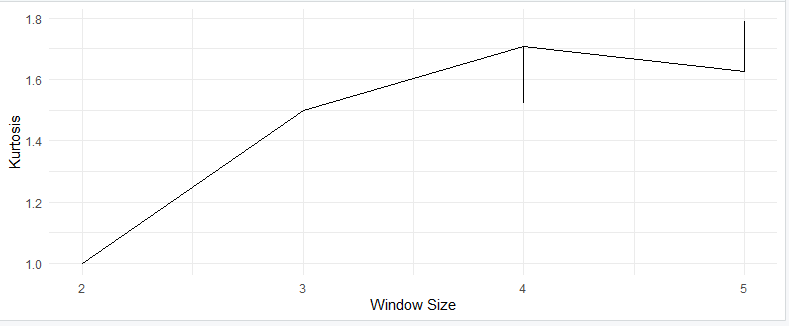
Kurtosis Plots

Kurtosis plots are also known as kurtograms. They provide a visual representation of how kurtosis changes with different window sizes in time series or signal data. To create a kurtosis plot in R, you can use the following code:

R code
# Load required libraries
library(moments) and library(ggplot2)
install.packages("moments")
library(moments) # For kurtosis calculation
install.packages("ggplot2")
library(ggplot2) # For creating the plot
# Sample data (replace this with your time series data)
data <- c(12, 15, 18, 22, 25, 28, 31, 35, 38, 41)
# Create a function to calculate kurtosis for a given window size
calculate_kurtosis <- function(data, window_size)
                         {
kurtosis_values <- numeric(length(data) - window_size + 1)
                                for (i in 1:(length(data) - window_size + 1))
                                                    {
window <- data[i:(i + window_size - 1)]
kurtosis_values[i] <- kurtosis(window)
}
           return(kurtosis_values)
}
# Specify a range of window sizes
window_sizes <- 2:5
# Adjust this range as needed
# Calculate kurtosis for each window size
kurtosis_data <- lapply(window_sizes, function(window_size)
                                                    {
kurtosis_values <- calculate_kurtosis(data, window_size)
                                                                                                  data.frame(WindowSize = rep(window_size, length(kurtosis_values)),
Kurtosis = kurtosis_values)
})
# Combine the results into a single data frame
kurtosis_data <- do.call(rbind, kurtosis_data)
# Create a kurtosis plot
ggplot(kurtosis_data, aes(x = WindowSize, y = Kurtosis)) +
geom_line() +
labs(x = "Window Size", y = "Kurtosis") +
theme_minimal()

This code generates a kurtosis plot that allows you to visualize how kurtosis changes with different window sizes in your time series data.

Here’s the output you will get from the code:
How to generate Different Types of Kurtosis Curves

Now, let’s explore how to generate different types of kurtosis curves in R. For this, we’ll use probability distribution functions that exhibit these behaviors.

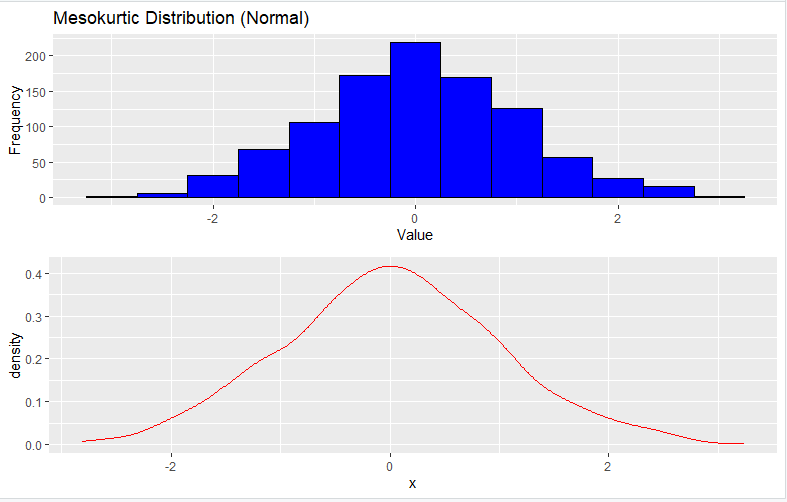
1. Mesokurtic Distribution (Normal)

To generate a Mesokurtic distribution, you can use the rnorm function, which generates random numbers from a normal distribution:

R code
# Set the seed for reproducibility
set.seed(123)
# Generate data from a normal distribution (Mesokurtic)
n <- 1000
# Number of data points
mean_val <- 0
# Mean of the normal distribution
sd_val <- 1
# Standard deviation of the normal distribution
data <- rnorm(n, mean = mean_val, sd = sd_val)
# Create a histogram to visualize the distribution
library(ggplot2)
# Plot the histogram
p <- ggplot(data.frame(x = data), aes(x)) +
geom_histogram(binwidth = 0.5, fill = "blue", color = "black") +
labs(x = "Value", y = "Frequency") +
ggtitle("Mesokurtic Distribution (Normal)")
# Create a density plot (trendline)
density <- ggplot(data.frame(x = data), aes(x)) +
geom_density(color = "red")
# Combine the histogram and density plot
library(gridExtra)
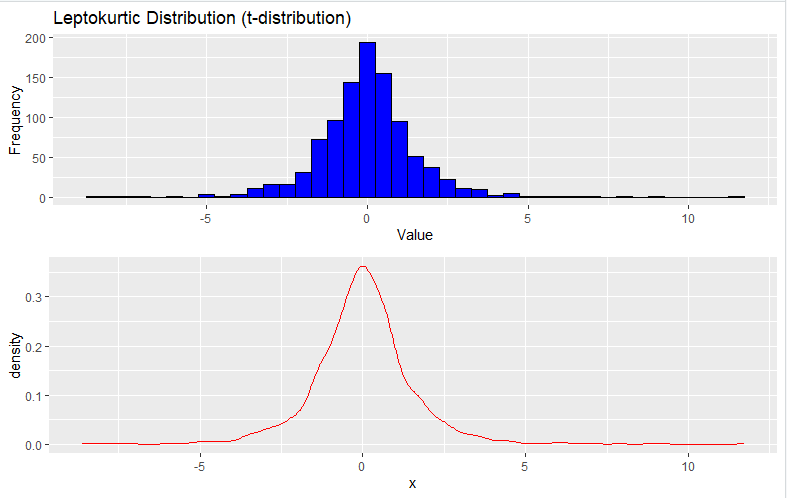
grid.arrange(p, density, ncol = 1)
Here’s the output you will get from the code:

2. Leptokurtic Distribution (t-Distribution)

To generate a Leptokurtic distribution, you can use the rt function to generate random data from a t-distribution with low degrees of freedom:

R code
# Set the seed for reproducibility
set.seed(123)
# Generate data from a t-distribution with low degrees of freedom (Leptokurtic)
n <- 1000
# Number of data points
df <- 3
# Degrees of freedom (adjust as needed)
data <- rt(n, df)
# Create a histogram to visualize the distribution
library(ggplot2)
histogram_plot <- ggplot(data.frame(x = data), aes(x)) +
geom_histogram(binwidth = 0.5, fill = "blue", color = "black") +
labs(x = "Value", y = "Frequency") +
ggtitle("Leptokurtic Distribution (t-distribution)")
# Create a density plot (trendline)
density_plot <- ggplot(data.frame(x = data), aes(x)) +
geom_density(color = "red")
# Combine the histogram and density plot
library(gridExtra)
grid.arrange(histogram_plot, density_plot, ncol = 1)
Here’s the output you will get from the code:

3. Platykurtic Distribution (Laplace Distribution)

To generate a Platykurtic distribution, you can use the rlaplace function to generate random data from a Laplace distribution:

R code
# Load required library
library(LaplacesDemon)
# For generating Laplace distributed data
library(ggplot2)
# For creating a histogram plot
# Set the seed for reproducibility
set.seed(123)
# Generate data from a Laplace distribution (Platykurtic)
n <- 1000
# Number of data points
data <- rlaplace(n, 0, 1)
# Adjust location and scale as needed
# Create a histogram to visualize the distribution
histogram_plot <- ggplot(data.frame(x = data), aes(x)) +
geom_histogram(binwidth = 0.5, fill = "blue", color = "black") +
labs(x = "Value", y = "Frequency") +
ggtitle("Platykurtic Distribution (Laplace)")
# Create a density plot (trendline)
density_plot <- ggplot(data.frame(x = data), aes(x)) +
geom_density(color = "red")
# Combine the histogram and density plot
library(gridExtra)
grid.arrange(histogram_plot, density_plot, ncol = 1)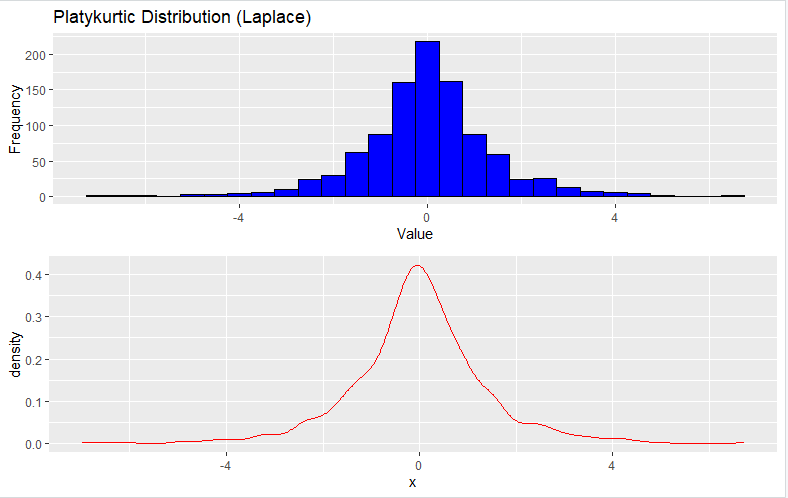
Here’s the output you will get from the code:
Practical Applications of Kurtosis

Kurtosis has several practical applications in data analysis and statistics. A few of them are listed below:

  • Risk Assessment in Finance: Kurtosis helps assess the risk and volatility of financial assets. Assets with high kurtosis are riskier due to more significant price swings.
  • Data Transformation: It helps decide whether data needs to be transformed to approximate a normal distribution. Log or Box-Cox transformations are often applied.
  • Data Ethics and Privacy: In data science, understanding kurtosis aids in handling sensitive data responsibly.

Conclusion: Unmasking the Secrets of Data’s Silhouette

In the intricate world of data, where numbers dance and patterns emerge, kurtosis is like the master storyteller who reveals the hidden tales within. It’s not just another statistic; it’s the torchbearer guiding us through the labyrinthine shapes of data distributions. With kurtosis by your side, you become the detective of data, distinguishing between the suave and the eccentric. It whispers the secrets of normalcy, heavy tails, and light tails, giving your data its very own personality. From the bustling floors of finance to the serene landscapes of data analysis, kurtosis stands as a trusty companion in your statistical odyssey. It’s the key to unraveling the mysteries, the secret sauce in your data science recipe, and the compass that keeps you on course in the wild terrain of probability distributions. So, as you embark on your data-driven adventures, remember that kurtosis is your ally—a beacon of insight in the twilight realm of data’s silhouette.